Sobre análisis de regresión

Porque analizar los residuos en una regresión? En una regresión la aleatoriedad y el carácter impredecible del error son fundamentales. Una ecuación de regresión, también llamado modelo tiene la forma siguiente

Y = (a+bx)+e

Done Y es la repuesta y X es el predictor, mientras que a es una constante y e el error, b es el factor multiplicativoo coeficiente del predictor que no es más que la pendiente de la línea que representa la ecuación. Esta fórmula es equivalente a decir que el modelo es tal que:

Repuesta = sistema determinista + sistema estocástico

La matemática define "sistema determinista a aquel en que el azar no está involucrado en el desarrollo de los futuros estados del sistema. Un modelo determinista producirá siempre la misma salida a partir de las mismas condiciones de partida o el estado inicial." Estocástico es el sistema que no es determinista.

En este caso (a+bx) es determinista mientras que que el error como dede ser es estocástico. La porción determinista del modelo se explica claramente por el predictor. Siendo el predictor, siempre que tome un mismo valor generará la misma repuesta. La aleatoriedad y el carácter impredecible del error es lo que llamamos estocástico. El error, también llamado residuo es la diferencia entre el valor predecible de la repuesta dada por la ecuación del modelo y el valor real de esta repuesta, como podemos observar en la figura siguiente. Esta diferencia debe ser impredecible ya que de lo contrario tendríamos parte de la porción determinista en el mismo error lo que le quitaría su carácter de estocástico.



La única forma de observar si esto es el caso o no es a través del análisis de los residuos. Parte crucial en el análisis de residuo es el la gráfica de valores ajustados (fitted value) o valores predecibles versus residuos. La suma de los residuos debe ser igual a zero, significando que los residuos deben ser centrado alrededor de cero, como observamos en la gráfica



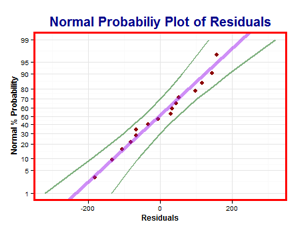
También es importante el normal probability plot para mostrar que la distribución de los residuos es totalmente normal. Los residuos adyacentes no deben guardar ninguna correlación entre ellos, en otras palabras no debe existir ningún patrón de los residuos en el tiempo.

 

Regresión es usada en análisis de varianzas ANOVA y en diseño de experimento DOE, en donde se debe determinar que tan ajustado a la data es el modelo. Por ello los estadísticos calculan la bondad de ajuste (goodness-of-fit). El coeficiente de determinación R-squared de la regresión es parte de estos cálculos. En general podemos decir que un modelo se ajusta bien a la data si las diferencias entre los valores observados y los valores esperados (calculados por la ecuación) son pequeñas, es decir si los residuos son pequeños y responden a las características que definimos arriba. El coeficiente de determinación mide la cercanía de la data a la línea ajustada de la ecuación de regresión. Representa el porcentaje de la variación de la repuesta encontrada en el modelo.

R squared = variación explicada/variación total. Donde 0% indica que el modelo no puede explicar la variación de las repuestas en cuanto a su media, y 100% indica que el modelo puede explicar toda la variabilidad presente. En teoría con R-squared igual a 100% todos los valores observados estarían exactamente en la línea ajustada de la regresión. Mientras más se alejan de esta recta de menos porcentaje será el coeficiente de determinación.



En la figura abajo observan la diferencia en la gráfica de un R squared de 38% a la izquierda y de 87% a la derecha.



Sin embargo usando el coeficiente de determinación como único indicador bueno y válido para la decisión de la predictabilidad del modelo es un error del analista. Existen casos de bajo % de R-squared con un modelo bueno y casos de alto % de R-squared con un modelo que no se ajuste a la data. Si el valor de R-squared es bajo pero los predictores son estadísticamente significantes se puede seguir apreciando el impacto de cualquier cambio en el predictor sobre la repuesta. En la teoría se define intervalos de criterios de aceptación para el valor de R- squared, pero que tan alto debe ser R-squared depende del rango de predicción que desea, si el proceso requiere o no una predicción precisa. El caso inverso se puede dar con un porcentaje alto del coeficiente de determinación y predictores que no son estadísticamente significantes donde no podemos concluir que el modelo es correcto. Los residuos como se ha dicho deben ser analizados. La significancia estadística de predictores se observa a través del cálculo del p-value, mayor o menor a 0.05

In conclusion R-squared nos provee un estimado de la potencia de la relación entre el modelo y la repuesta pero no concluye formalmente sobre la hipótesis de significancia estadística de dicha relación. Dicho esto en una ANOVA o un DOE podemos tener uno de los cuatros casos siguientes:

1- Alto R-squared alto p-value
2- Alto R-squared bajo p-value
3- Bajo R-squared bajo p-value
4- Bajo R-squared alto p-value

El valor-p de cada factor o predictor prueba la hipótesis nula de que el coeficiente del predictor es cero y la alterna es que no es cero. Un coeficiente cero significa que bx es cero pro lo tanto el predictor no no es significante. En pocas palabras un factor del DOE es significante cuando el p-Value es menor a 0.05 porque es cuando aceptamos la hipótesis nula de que el coeficiente b no es cero y por lo tanto bx tiene un impacto sobre la repuesta. El coeficiente representa la media de cambio en la repuesta para un cambio unitario del predictor. Un factor es insignificante cuando el p-Value es mayor a 0.05 indicando que cambios del predictor o factor no son asociados con cambios en la repuesta. El análisis siguiente muestra que los factores "responsive to calls" y "ease of communication" son significantes pero que "customer type 2 y customer type 3" no lo son y por lo tanto deberíamos removerlos de la regresión es decir en este caso del DOE como podemos observar en la segunda tabla de análisis.

[/img]

" />

La clave para asimilar este concepto de significancia es visualizar el coeficiente b como la pendiente. Mientras menos inclinada positivamente o negativamente esta la pendiente menos (es decir mientras más pequeño el valor del coeficiente) menos significancia tendrá sobre la repuesta y por ende mayor será su p-Value. Una pendiente nula, es decir una recta totalmente horizontal dice que cualquier cambio del factor no implica ningún cambio en la repuesta. En la ecuación y la tabla arriba el coeficiente de "responsive to call" es de 0.435673 indicando que por cada puntuación adicional en la encuesta sobre responsive to call podemos esperar que la satisfacción del cliente aumente de 0.435673 puntos asumiendo un "ease of comunicación" fijo.

En un análisis de regresión, un DOE nos gustaría tener la condición 2 de alto coeficiente de determinación y bajo p-value, es decir un modelo bien ajustado y factores estadísticamente significantes. Pero que pasa si su condición es la primera: alto R-squared, alto p-value o su condición es la tercera bajo R-squared bajo p-Value? Condición una alto R-squared alto P- value significa que el modelo ajusta perfectamente pero los factores no son significantes. Esto es una aberración. No se está midiendo la repuesta correctamente. Este caso no existe. La condición 3 bajo R-squared bajo p-Value significa que el modelo de regresión tiene variables significantes pero explica poco de la variabilidad. Esta situación es muy posible.

Usemos este ejemplo de Altura y peso en una raza de perros tomando las hembras como un subgrupo a parte de los machos, con una ecuación de regresión linear prácticamente igual pero el de la izquierda con un coeficiente de determinación bajo y el de la derecha con el coeficiente de determinación alto. Prácticamente la ecuación de regresión es y= 45+2x nos dice que por cada centímetro de crecimiento en altura el peso del perro aumentará de dos libras.



En el modelo izquierdo R-squared es bajo 21.79% y con un p-Value bajo de 0.0006 como muestra el análisis siguiente indicando que el predictor o factor es significante. La data proviene de las hembras.



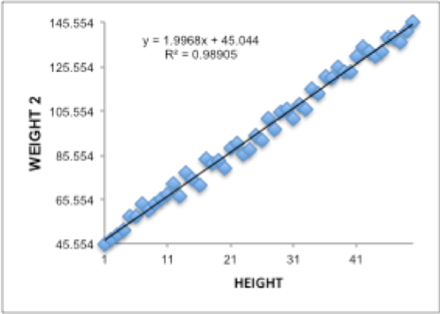
Mientras que en el modelo derecho de los machos tenemos la condición ideal del R-squared alto 98.9% y un p-Value bajo de 0.0000 en la tabla siguiente. En el gráfico podemos observar que la pendiente positiva es alrededor de dos unidades y que siguen la tendencia que existe en las repuestas. El p-Value de los dos modelos nos indica que debemos rechazar la hipótesis nula que el producto coeficiente-factor no tiene efecto, es insignificante, y falla a favor de la hipótesis alterna admitiendo que si bx tiene significancia estadística sobre la repuesta peso.



El modelo izquierdo de las hembras nos dice que tenemos menos precisión en la predicción probablemente por otros factores como número de veces que ha parida que no se está contemplando en la regresión. Para apreciar la precisión debemos observar los intervalos de confianza y los intervalos de predicción, el último siendo el rango más probable de contener la repuesta de cada cambio en el predictor. Mientras más estrecho el rango mayor precisión en la predicción del modelo. Observamos el amplio rango del modelo 1 debido al bajoR-squared



En conclusión no todo el tiempo un R-squared bajo es malo y tampoco un alto es bueno. Analizan siempre los residuos y entienden que tanta precisión se requiere para la predicción. No necesariamente un coeficiente de determinación bajo, implica que los factores de un diseño no son significantes, y vice versa para un coeficiente de determinación alto. Se puede tener significancia estadística aún con alta variabilidad en la repuesta.Todo es cuestión de la precisión con la cual queremos predecir los eventos en el proceso. En algunos casos puede ser que haya uno o más factores que no se han contemplado en el modelo.

La data usada para la regresión sobre el caso de los perros es la siguiente.